Binding Energy
The nuclear source of energy is understood only if the concept of binding energy (BE) is understood. The nucleons, as said, are held by short-range nuclear forces. The mass of a nucleus is generally less than the sum of the masses of the nucleons. This difference is called the mass-defect. Such a phenomenon is observed in atomic or subatomic levels, and not with ordinary materials that we handle, where the total mass has to be the sum of the component masses. The mass-defect is responsible for the binding together of the nucleons. The energy equivalent of the mass-defect is called the binding-energy of the nucleus. Look at the following illustrative picture and visualize that, when individual nucleons pack themselves together to form a system, which we call nucleus, they liberate some energy in the form of photons (gamma rays). The liberated energy manifests as a reduction in the net mass of the nucleus, as per Einstein’s relation. It may also be said that the nucleus could be split into nucleons by supplying external energy equal to the binding energy.
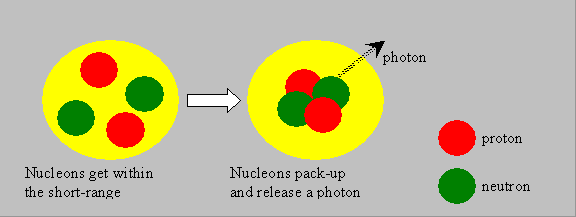
|
Example: For the He-4 nucleus, the binding energy may be computed as below: Total mass of 2 protons = 2 ´ 1.00728 = 2.01456 amu Total mass of 2 neutrons = 2 ´ 1.00866 = 2.01732 amu Total mass of nucleons = 4.03188 amu Mass of Alpha particle (measured) = 4.00153 amu Mass defect Dm = 0.03035 amu Hence, Binding energy of He-4 = 28.3 MeV. ( i.e. 0.03035 amu ´ 931.5 MeV/amu)
|
The enormity of the nuclear binding energy can be better appreciated by comparing it to the binding energy of an electron in an atom. The nuclear binding energies are on the order of a million times greater than the electron binding energies of atoms. For example, the binding energy of an electron to the nucleus in the hydrogen atom is 13.6 eV, whereas the binding energy of nucleons in the He-4 nucleus is 28,300,000 eV (roughly 2 million times!)
Binding Energy Per Nucleon (BE/A): As the number of particles in a nucleus increases, the total binding energy also increases. The rate of increase, however, is not uniform. This lack of uniformity results in a variation in the amount of binding energy associated with each nucleon within the nucleus. This variation in the binding energy per nucleon (BE/A) is easily seen when the average BE/A is plotted versus atomic mass number (A), as shown in the figure below:
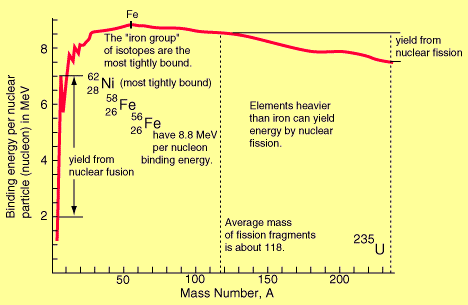
Binding Energy per Nucleon vs. Mass Number
The above figure illustrates that as the atomic mass number increases, the binding energy per nucleon decreases for A > 60. The BE/A curve reaches a maximum value of 8.79 MeV at A = 56 and decreases to about 7.6 MeV for A = 238.
The general shape of the BE/A curve can be explained using the general properties of nuclear forces. As already said, very short-range attractive forces that exist between nucleons hold the nucleus in its shape. On the other hand, the long-range repulsive electrostatic (coulomb) forces that exist between all the protons in the nucleus continuously tend to force the protons apart, thus splitting the nucleus. As the atomic number (Z) increases, the repulsive electrostatic forces within the nucleus increase. To overcome this increased repulsion and maintain stability, the proportion of neutrons in the nucleus must increase. This increase in the neutron-to-proton ratio only partially compensates for the growing proton-proton repulsive force in the heavier, naturally occurring elements. As the repulsive forces are increasing, less energy must be supplied, on the average, to remove a nucleon from the nucleus. In other words, the BE/A has decreased. The BE/A of a nucleus is an indication of its degree of stability. Generally, the more stable nuclides have higher BE/A than the less stable ones. The increase in the BE/A as the atomic mass number decreases from 260 to 60 is the primary reason for the energy liberation in the fission process. In addition, the increase in the BE/A as the atomic mass number increases from 1 to 60 is the reason for the energy liberation in the fusion process, which is the opposite reaction of fission.
The heaviest nuclei require only a small energy addition for the relatively large coulomb forces to overcome the attractive nuclear forces, in order to split the nucleus into two halves. Consequently, the heaviest nuclei are easily fissionable compared to lighter nuclei. The addition of the energy required to cause a distortion in the heavy nucleus leading to fission, is commonly achieved by adding a neutron into the nucleus. Some nuclei experience chances of undergoing fission, even without adding a neutron, such a phenomenon being called ‘Spontaneous fission’.
In the fusion of Deuterium (a hydrogen isotope H-2) and Tritium (another hydrogen isotope H-3), called the D-T fusion, the total energy released is 17.6 MeV. In the fission of U-235 by neutron, the energy released is about 200 MeV. Though fission energy seems higher, the release of energy per unit mass of the fuel, is much higher in the case of fusion than in fission. More discussion on fission and fusion will be given later.